Ένα σώμα μάζας 3kg, θεωρείται υλικό σημείο, αμελητέων διαστάσεων και ισορροπεί στη θέση Α, όπως στο σχήμα, δεμένο στο κάτω άκρο ενός κατακόρυφου ιδανικού ελατηρίου, με φυσικό μήκος lο=0,9m και σταθερά k=80Ν/m, το άλλο άκρο του οποίου έχει προσδεθεί στο κέντρο Ο, ενός λείου κατακορύφου κυκλικού οδηγού, ακτίνας R=1m.
i) Να υπολογιστούν τα μέτρα των δυνάμεων που ασκούνται στο σώμα στη θέση Α.
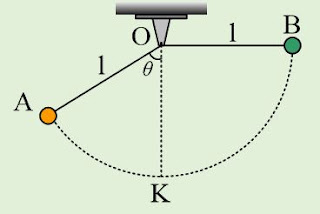
Δυο μικρές σφαίρες Α και Β, αμελητέων διαστάσεων, είναι δεμένες στα κάτω άκρα δύο αβαρών και μη εκτατών νημάτων, με το ίδιο μήκος l=2m, τα άλλα άκρα των οποίων έχουν δεθεί σε σταθερό σημείο Ο. Εκτρέπουμε την σφαίρα Α κατά γωνία θ (όπου ημθ=0,8 και συνθ=0,6) και την σφαίρα Β στην αντίθετη πλευρά, ώστε το νήμα να γίνει οριζόντιο, όπως στο σχήμα. Σε μια στιγμή αφήνουμε ελεύθερη την σφαίρα Β και μετά από λίγο και την σφαίρα Α. Οι δυο σφαίρες συγκρούονται στην θέση Κ, όπου τα νήματα γίνονται κατακόρυφα. Η Α σφαίρα έχει μάζα 0,4kg και μετά την κρούση κινείται προς τα αριστερά, με αποτέλεσμα το νήμα εκτρέπεται κατά μια μέγιστη γωνία φ, όπου συνφ=0,75. Ζητούνται:
i) Ο αρχικός ρυθμός μεταβολής της στροφορμής της σφαίρας Α, αμέσως μόλις αφεθεί να κινηθεί, ως προς το σημείο Ο.
ii) Η στροφορμή της σφαίρας Α και ο ρυθμός μεταβολής της, ως προς το Ο, ελάχιστα πριν την κρούση των δύο σφαιρών.
iii) Το μέγιστο μέτρο του ρυθμού μεταβολής της στροφορμής της σφαίρας Α, ως προς το Ο, μετά την κρούση.
iv) Η μεταβολή της στροφορμής ως προς το Ο της σφαίρας Β, η οποία οφείλεται στην κρούση.
Δίνεται g=10m/s2
ή
Δυο σώματα Σ και Σ1, με μάζες m=2kg και Μ=4kg είναι δεμένα στα άκρα ενός ιδανικού ελατηρίου (αρκετού μήκους) σταθεράς k=50Ν/m. Τα σώματα ηρεμούν σε οριζόντιο επίπεδο, το οποίο χωρίζεται σε δυο περιοχές Α και Β, όπου το τμήμα Α είναι λείο, ενώ το Β όχι, με το ελατήριο στο φυσικό μήκος του. Κρατώντας ακίνητο το σώμα Σ1, εκτρέπουμε το σώμα Σ προς τα αριστερά συμπιέζοντας το ελατήριο κατά d1=0,4m και το αφήνουμε να ταλαντωθεί την στιγμή t0=0, ενώ αφήνοντας ελεύθερο το Σ1, παρατηρούμε ότι παραμένει ακίνητο.
i) Θεωρώντας την αρχική απομάκρυνση θετική, να βρεθεί η εξίσωση της απομάκρυνσης του Σ σε συνάρτηση με το χρόνο (x=x(t)).
ii) Να κάνετε την γραφική παράσταση της τριβής, η οποία ασκείται στο σώμα Σ1, σε συνάρτηση με το χρόνο.
iii) Αν επαναλάβουμε το πείραμα αυξάνοντας την αρχική εκτροπή του σώματος Σ, παρατηρούμε ότι η μέγιστη εκτροπή, για την οποία δεν παρατηρείται μετακίνηση του Σ1, είναι d2=0,5m. Να βρεθεί ο συντελεστής οριακής στατικής τριβής μεταξύ του επιπέδου Β και του σώματος Σ1.
iv) Αν μεταξύ του σώματος Σ1 και του επιπέδου Β αναπτυσσόταν τριβή με συντελεστές μ=μs=0,2 και εκτρέπαμε ξανά το σώμα Σ κατά d2, να υπολογιστεί το συνολικό διάστημα που θα διανύσει το σώμα Σ1, μέχρι να σταματήσει, αν το σώμα Σ ταλαντώνεται τελικά με πλάτος Α3=0,35m.
Δίνεται g=10m/s2, ενώ κάθε σώμα κινείται στο τμήμα του επιπέδου που βρίσκεται αρχικά.
ή
Ένα σώμα μάζας 3kg, θεωρείται υλικό σημείο, αμελητέων διαστάσεων και ισορροπεί στη θέση Α, όπως στο σχήμα, δεμένο στο κάτω άκρο ενός κατακ...
